Mutualism & Sampling Theory

Can Either Stand Up To g Theory?

Nagivation:

‒Sampling Theory
‒Mutualism
—Is IQ Cultural?
—Age De-Differentiation
—Matthew Effects
—SES & Learning
—The FLynn Effect
—Longitudinal & Experimental Evidence
‒Conclusion
‒References

This post is a response to Sasha Gusev’s inept reading [1] of the factor-analytic literature.

To begin, the strength of the g factor isn't that it explains high proportions of the variance in a test battery. Rather, what's typically replicated [2, pp.79 & 81[ is that it explains more variance than all other factors put together. Suppose you made a 10-question vocabulary test and then randomly split it into two 5-question vocabulary tests and found that the two vocabulary tests correlated at only .3. Would you fault IQ if it explained less than 50% of the variance in either test? No, you'd congratulate it if it completely explained the correlation between vocabulary tests; IQ explained performance on the tests in proportion to the extent that the tests were real to begin with. Of the common factor variance in a test battery, the non-g residuals you're left to play with are a pittance.

Sampling Theory:

>"Multiple theoretical accounts of the positive manifold can produce the same model fit."

Sure, multiple empirically-falsified ones. Let's deal with sampling theory first. Suppose we had 4 subtests, subtests 1, 2, 3, & 4, which suffer maximally from such sampling problems such that each are evenly the result of 2 out of 4 uncorrelated mental abilities: ability a, b, c, & d; test 1 is c+a, test 2 is a+d, test 3 is c+b, and test 4 is b+d:

If we took any two tests (e.g. test 2 and test 4) and looked at what they had in common, a factor common to the two would be a purer expression of d while by contrast, a and b would become specificities which cancel out. That is, a factor solution which maximizes simple structure should minimize such sampling problems.

You may be jumping for joy hearing praise for the simple structure concept, but here's the thing. A variable, otherwise understood as a vector, can be understood as being a line in geometric space, and given the normalization of those variables, their correlation is equal to the cosine of the angle between the vectors:

As such, the correlations among groups of variables can be understood as the angles between sets of intersecting lines in geometric space, with a correlation of zero being an angle of 90 degrees and correlation of 1 being an angle of zero degrees. The consequence of this is that for a positive manifold, a proper simple structure solution shouldn't assume orthogonality. Within a two-dimensional principal component space, the angles between variables (i.e. between blue dots / dotted black lines) will look less like image A and more like image B:

If the dots from image B were forced to use the factors from image A, then the lines that were originally closer to green than to purple will continue to be so, but we'd introduce two problems, the first being that the variability in factor loadings that variables have across factors would be artificially limited; where an oblique solution is most appropriate, the variables that rightly belong on an oblique factor won’t correlate as highly with the factor’s orthogonal counterpart. The second ironically enough happens as a consequence of factor rotation being done with the goal of maximizing the variability in factor loadings that variables have, this being that a general factor will always be partitioned into group factors regardless of how arbitrarily-highly correlated the variables of any two group factors happen to be. In principle, a solution with arbitrarily-high factor-factor correlations should be accepted so long as it sufficiently increases the factor-variable correlations.

This allows us to test for an interesting property, one which is not merely the consequence of a positive manifold. Suppose two models were fitted, one which attempts to find the best possible oblique simple structure, and another which has the same goal but with an additional restriction that the factor-factor correlations must be perfectly reproduced by a single general factor. If the two models had equivalent fit, this would suggest there's something real about the general factor and that it's not merely the consequence of a positive manifold; this would mean that a hierarchical model would achieve the univariate equivalent of simple structure. As it happens, this has been tested multiple times over [3], and the fit differences are always insignificant when comparing hierarchical models to the oblique models that they're derived from. Especially impressive is that this is true of the Woodcock-Johnson test battery, whose content is based on Carol's comprehensive taxonomy of cognitive abilities.

As it turns out, when abilities a, b, c, and d are expressed with minimal such sampling problems, they all share exactly the same common properties rather than being independent. Supposing that something like brain size were causal for performance on every test while something like neuron health were also causal for performance on every test despite brain size and neuron efficiency being uncorrelated (i.e. despite brain size and neuron efficiency failing to comprise any "neuro-g"): It would have to be that the two traits vary by the same proportions in how causal they are for different test performances, leaving the unidimensionality of intelligence sensible at the psychological level of analysis even though the different performance-causing traits aren't correlated with each other. What matters is whether different neural traits have different causal effects on different abilities, not whether different neural traits are uncorrelated. This is repeatedly shown, e.g., when looking at genetic correlations between different abilities (both twin-based and molecular-based genetic correlations), all despite genetic variation very clearly being extremely multidimensional [4, 5, 6, 7, 8, 9, 10, & 11]. This should also be a case against Mutualism! Almost all SNPs impact item responses in accordance with a factor model of traits rather than the patterns predicted by network models. Traits are how genes get to act on the world!

The insignificant differences in model fit are in spite of it being mathematically impossible for a hierarchical model to fit better than the oblique model it's derived from. An oblique model has total freedom to set the factor-factor correlations however it pleases while a hierarchical model has no such freedom, thereby showing said freedom to be of no advantage. In comparisons between the two then, the best a hierarchical model can hope for is equality, which is what we observe. By contrast, if hierarchical models are abandoned, g theory does have one theoretical advantage. Suppose we had two vocabulary tests again, but this time suppose one were comprised of questions about analogies between words. One might regard the analogies test as requiring more higher-order thought, even if the two vocabulary tests are more similar than what's implied by their g-loadings. However, hierarchical models can't exploit this due to an artificial proportionality restriction, where variables can only load on the general factor in proportion to their loading on their group factor. When this proportionality restriction is relaxed in bifactor models, the bifactor models routinely fit meaningfully better than the hierarchical models, even with fit indices which penalize model complexity [see 12 & 13].

Spearman argued from the earliest days that his test of vanishing tetrads could trivially be made to fail if the same test was entered into a correlation matrix multiple times over, but in his day, the matter was unresolvable due to the subjectivity of whether two different tests share the same content. Now however, simple structure seems to be a convenient way of determining objectively which tests should be grouped together. Instead of multifactor models fitting slightly better due to residual correlations between specificities, there's a strong case that Spearman was right about failures being due to multiple tests loading on the same specificities [see 3].

Mutualism:

The meat of Gusev's post here is his case for mutualism, and his case rests on confusion over the predictions of different theories as well as the state of the evidence.

Is IQ Cultural?

Part one isn't even relevant to whether intelligence is unidimensional, it's just an assertion that it's cultural. I guess this is the "I hate IQ" thread and not the thread about how "I believe in a specific theory and think that g is mistaken due to contradicting it". But I'll bite. Verbal ability is highly g-loaded, but the taxonomy of cognitive tests is vast, and variability in g-loadings isn't reducible to variability in verbal content. Kan's findings [14 & 15] that subtest g-loadings correlate with the proportion of content changed for international translations is probably the result of the correlation with verbal content in the Wechsler tests he uses. This is probably just a peculiarity of the WISC however, as the opposite finding has been observed to be the case for other batteries [16].

Age De-Differentiation:

In part two, Gusev is right to bring up the age de-differentiation literature, seeing as one of the key predictions of mutualism theory is that tests should become more correlated with time. A general-factor theory should mostly disagree, albeit with the caveat of crystallized content, since if intelligence is causal for learning ability, then unrelated aspects of factual knowledge should become more correlated as they're introduced to a fresh audience and all aspects of factual knowledge are increasingly influenced by the same unitary cause of knowledge. Interestingly enough, in the grade school sample of the very paper that Gusev cites, there is no trend aside from gc (i.e. crystallized knowledge) and gv. It's funny that Gusev should bring up Spearman's law of diminishing returns (i.e. that tests are less correlated at the higher end of the ability distribution), because it strikes me that this is precisely the opposite of the prediction you should make if you believed in mutualism theory. If gains in one ability are causal for gains in another, you should expect groups of people who haven't undergone the nuclear chain reaction to be those who have the smallest correlations. That the opposite is the case has been known since the earliest of days, and has been replicated hundreds (literally 408) times [17].

How does the age de-differentiation literature stack up? Well, there was another recent meta-analysis [18] finding that tests become less correlated with age among children before becoming more correlated with age among adults. It seems to me that this is merely what one would expect from Spearman's law of diminishing returns, since children develop biologically whereas the fluid intelligence of adults slowly declines with age [19].

Aaaaage de-differentiation was a question people started investigating before anybody realized it was relevant to the question of mutualism, but Gignac also looked into it again a while ago this time realizing the relevance (I'm bringing it up here because his analyses don't seem to be included in the meta-analysis); Gignac's results are as follows [20, p.95]:

Matthew Effects:

In part three, it's hilarious that Gusev should bring up the non-existence of a matthew effect, as if different abilities are mutualistically self-reinforcing, this should bring about a matthew effect where 'intelligence' is causal for the ability to acquire more intelligence. He's right of course, an enormous meta-analysis found that the stability of g over the course of one's life can realistically be regarded as a cross-time correlation of over .9 [see 21].

Now how about the supposed failure of IQ to predict learning ability? Well, I've actually written about this before [see 22]: When you ask somebody to learn about something to see how well or fast they learn it, this takes an enormous amount of investment on their part, there's an enormous degree of specificity (as well as methodological problems with measuring learning) within any one learning task, and if you try to make somebody complete two separate learning tasks, the two will correlate exceedingly poorly. It's the problem of the two vocabulary test all over again, only more extreme. Still, there are real effects. A meta-analysis [23] of effects of IQ on responses to reading instruction found a significant bivariate correlation of r = +0.17. Now, what happens when we make people go through a long, arduous process of learning many different things, and factor analyze correlations between time to learn, ability asymptotes, etc? Well, to the extent that general learning ability is a trait that actually even exists, general intelligence correlates with it at over .9 [22].

Keep in mind also that this entire literature is all under conditions of top-down instruction. On top of such straightforward responses to instruction, we have strong reason to believe that IQ is causal for (or rather an enabler of) curiosity [22 & 24].

Gusev also randomly makes an unsourced remark that "IQ also can't predict cognitive decline." This is just wrong. Fluid intelligence increases up until puberty before slowly declining with age while crystalized intelligence continues increasing as people learn new stuff, and in the best study we have on this subject, not only did higher initial fluid intelligence predict lower declines in fluid intelligence and higher increases in crystalized intelligence, but stronger declines in fluid intelligence predicted lower increases in crystallized intelligence [19].

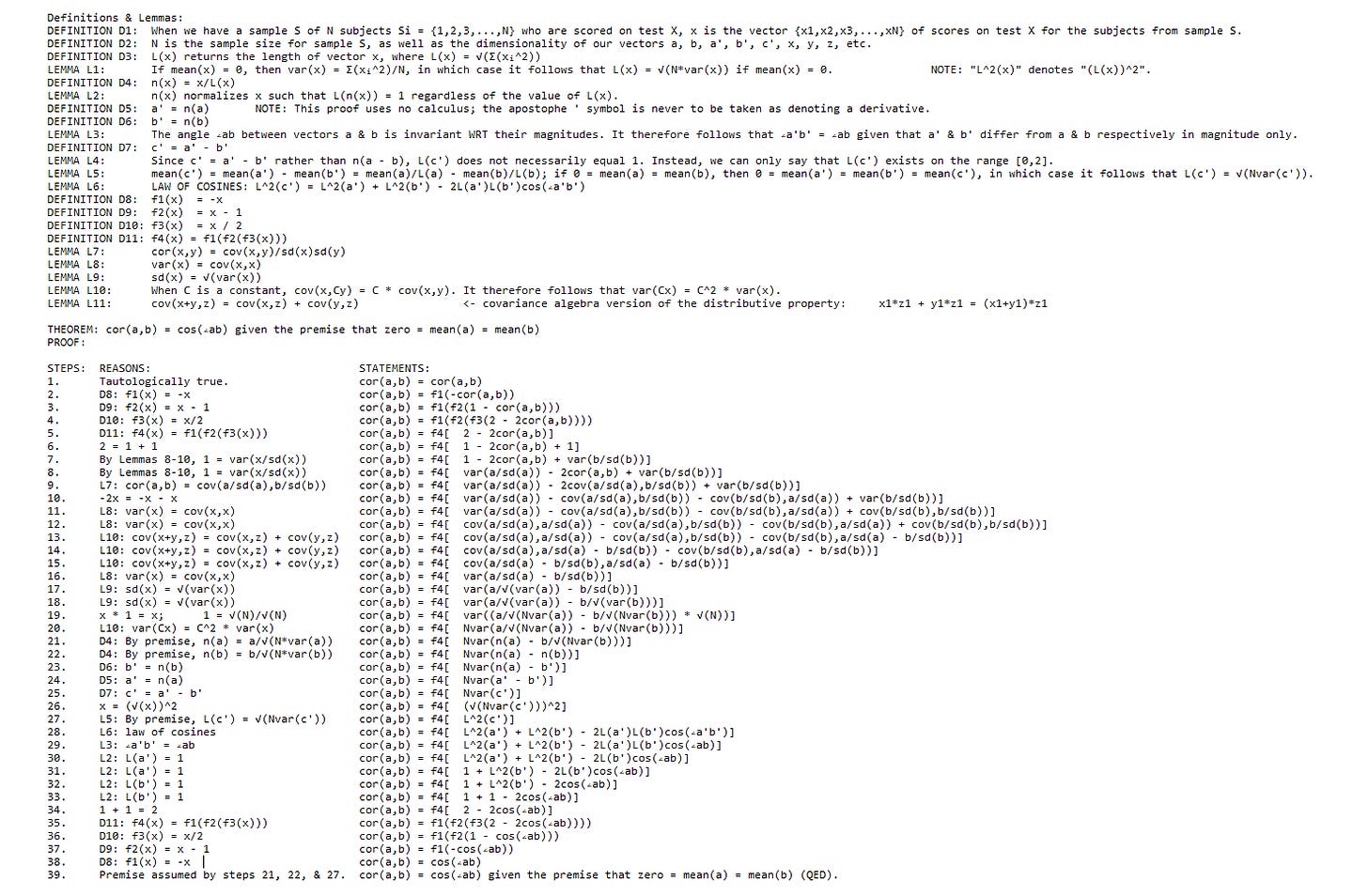
It's impressive that there's even the statistical power to test this given just how stable intelligence is with age, but this is the case nonetheless. Mutualism puts itself at contradiction with the fluid-crystallized theory of intelligence that a four year old could come up with. Which, btw: No, fluid and crystallized intelligence are only two group factors within the CHC taxonomy, and with all group factors taken together, the usual finding of equivalent model fit is observed, the fluid-crystallized distinction isn't proof of some alternate theory of intelligence from g theory, and the two correlate at over 0.8 to begin with [25].

Gusev also bizarrely denies that IQ is a measure of processing speed. No, if you show people an image of two lines for increasingly small fractions of a second, IQ correlates with at -.54 with the amount of time it takes somebody to be able to discern which one of the lines is longer than the other [26].

SES & Learning:

In part four, Gusev wants to eat his cake and keep it too, claiming that diverging SES is associated with diverging amounts of learning, with this being responsible for any correlation between IQ and learning rates, apparently forgetting that he had just claimed IQ to have no correlation with rates of learning. Is it non-existent or is it confounded? You can't have it both ways. In any case, there's a natural test for his question of confounding. Wealth and educational quality are some of those things that you can assign to people experimentally. We have multiple voucher studies where poor kids who apply for a voucher to attend better schools are randomly selected and compared in their test scores against non-selected applicants, including one which also moved them to live in different neighborhoods entirely; these find no significant effects [22].

This also speaks to effects of living in a smart culture. Presumably, this forces kids to make friends with the smarter kids of a smarter school, if this cultural effect matters it should be reflected in the voucher results. Speaking of which, we also have a 2019 longitudinal study finding the IQ of one's friend group not to predict changes in one's intelligence when controlling for initial scores [27].

The FLynn Effect:

In part 5, Gusev says the following:

"Mean IQ in the population has been increasing over generations, with some studies showing the increase happening on more g/culture loaded subtests and among lower scorers and even within families."

As it happens, there was a meta-analysis on this question, and when you don't ignore vast swathes of the literature, it's repeatedly found that precisely the opposite is the case; the correlation is -.38 [28]. One further qualification we can make is that more g-loaded tests tend to be a bit more difficult and that people are more inclined to guess randomly during conditions of high difficulty. People have been guessing more frequently over time, and as it happens, there are quantitative ways of assessing changes due to guessing, and when correcting for these, the correlation with score gains is -.47, and with 5 other necessary corrections, the correlation rises to -.82 [29]. We can do better than this basic analysis however.

What if we looked at studies assessing the changes for measurement invariance? We see repeated violations of scalar invariance [30, 31, 32, 33, 34, 35, 36, 37, 38, & 39], with biases systemically favoring newer samples [31, 32, 33, 35, 36, 37, & 38]. Flynn effects corrected for these biases either reduce substantially [31, 33, 35, 36, 37, & 39], vanish entirely [34], or reverse in direction [32 & 33]. Some tests also have questions ordered randomly rather than putting them in order of difficulty. In the olden days, people would just answer in chronological order, while nowadays, a larger percentage of people's incorrect answers appear at the beginning of the tests. In another study correcting for this and using only the items which display scalar invariance, no clear evidence was found for a long-term rise since the 1930s [40].

Without even correcting for measurement changes, we've also been running up against the limits of what gains are possible in the last decade or two, and raw scores have begun to decline in some of the most developed countries [41 & 42].

Longitudinal & Experimental Evidence:

Gusev then asserts that there's more longitudinal evidence for mutualism. I accept the study design as it concerns adults (although maybe I shouldn't since people with higher initial scores have smaller fluid declines), but the stability of IQ over time is too strong for a 1-2.5 year delay to be acceptable. As it concerns children however, children mature with age, and the children with higher initial scores have accelerated changes in ability & in neural development [43]. As such, given global increases in a single ability which causes all test performances, the findings among children aren't something that should be unexpected from the perspective of a g model. The only disagreement should be on age de-differentiation.

Gusev then brings up an experimental study [44]. Right out of the gate, the paper remarks that it's trying to challenge the rest of the literature, in which training in one domain is repeatedly found not to transfer to gains in other domains (the study is even literally titled "Looking for transfer in all the wrong places"). The paper's contention is that training in one area should only have the effect of expediting gains from training in another area as opposed to generalizing directly i.e. the assertion is that training gains should only generalize to other things that are being trained concurrently. This would immediately cause problems for mutualism in accounting for things which people don't go out of their way to train, like reaction time, but let's humor Gusev and see if the paper even supports its assertions. So, the target variable they're trying influence is a working memory test, their three experimental groups are trained on... working memory tests, and the control group is the only group trained on something other than a working memory test. And they find that the control group was the only one not to perform better on the target task. So, they find in their paper yet again that training doesn't generalize across domains. Incredible. Their sample size was also 90, with 10 participants withdrawing before the end of the study, leaving 20 participants per group. This is below the most lenient sample size guidelines I can find for even the most basic type of RCT, let alone one which looks at within-participant changes, which requires more power.

I was going to bring up the failure of the training literature myself but Gusev seems to have done my job for me. In any case, Gusev's paper has good reason to view the training literature [45] this way; researchers routinely fail to find any far-transfer effects to cognitive training. The meta-analytic effect is null, and moreover, effects have little to no heterogeneity beyond what can be expected of random error [45], thereby suggesting that it is not just a matter of certain training methods being effective while others are counter-productive.

Conclusion:

TLDR: Sampling theory is wrong, mutualism is wrong, and g exists psychologically. It is for good reason that g-factor theory is the overwhelming consensus of the relevant experts [46].

References:

1. Gusev, S. [@SashaGusevPosts]. (2024, May 11). I've written the first part of a chapter on the heritability of IQ scores. Focusing on what IQ is attempting [Tweet]. Twitter. Retrieved from https://x.com/SashaGusevPosts/status/1789493658116366704

2. Jensen, A. R. (1998) The g factor: The science of mental ability. Westport, CT: Praeger, Vol. 648. Retrieved from https://emilkirkegaard.dk/en/wp-content/uploads/The-g-factor-the-science-of-mental-ability-Arthur-R.-Jensen.pdf

3. Norman, G. (2024). Factor Analyses Of Mental Abilities: Oblique VS Hierarchical Model Fit. Half-Baked Thoughts. Retrieved from https://werkat.substack.com/p/factor-analyses-of-mental-abilities

4. de la Fuente, J., Davies, G., Grotzinger, A. D., Tucker-Drob, E. M., & Deary, I. J. (2021). A general dimension of genetic sharing across diverse cognitive traits inferred from molecular data. Nature Human Behaviour, 5(1), 49-58. Retrieved from https://sci-hub.ru/https://doi.org/10.1038/s41562-020-00936-2

5. Plomin, R., & Kovas, Y. (2005). Generalist genes and learning disabilities. Psychological bulletin, 131(4), 592. Retrieved from https://sci-hub.ru/https://doi.org/10.1037/0033-2909.131.4.592

6. Davis, O. S., Haworth, C. M., & Plomin, R. (2009). Learning abilities and disabilities: Generalist genes in early adolescence. Cognitive neuropsychiatry, 14(4-5), 312-331. Retrieved from https://sci-hub.ru/https://doi.org/10.1080/13546800902797106

7. Trzaskowski, M., Davis, O. S., DeFries, J. C., Yang, J., Visscher, P. M., & Plomin, R. (2013). DNA evidence for strong genome-wide pleiotropy of cognitive and learning abilities. Behavior genetics, 43, 267-273. Retrieved from https://sci-hub.ru/https://doi.org/10.1007/s10519-013-9594-x

8. Plomin, R., & Spinath, F. M. (2004). Intelligence: genetics, genes, and genomics. Journal of personality and social psychology, 86(1), 112. Retrieved from https://sci-hub.ru/https://doi.org/10.1037/0022-3514.86.1.112

9. Panizzon, M. S., Vuoksimaa, E., Spoon, K. M., Jacobson, K. C., Lyons, M. J., Franz, C. E., ... & Kremen, W. S. (2014). Genetic and environmental influences on general cognitive ability: Is g a valid latent construct?. Intelligence, 43, 65-76. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2014.01.008

10. Shikishima, C., Hiraishi, K., Yamagata, S., Sugimoto, Y., Takemura, R., Ozaki, K., ... & Ando, J. (2009). Is g an entity? A Japanese twin study using syllogisms and intelligence tests. Intelligence, 37(3), 256-267. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2008.10.010

11. de la Fuente, J., Davies, G., Grotzinger, A. D., Tucker-Drob, E. M., & Deary, I. J. (2019). Genetic “general intelligence,” objectively determined and measured. bioRxiv, 766600. Retrieved from https://www.biorxiv.org/content/10.1101/766600v3.full.pdf

12. Cucina, J., & Byle, K. (2017). The bifactor model fits better than the higher-order model in more than 90% of comparisons for mental abilities test batteries. Journal of Intelligence, 5(3), 27. Retrieved from https://sci-hub.ru/https://doi.org/10.3390/jintelligence5030027

13. Gignac, G. E. (2016). The higher-order model imposes a proportionality constraint: That is why the bifactor model tends to fit better. Intelligence, 55, 57-68. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2016.01.006

14. Kan, K. J., Wicherts, J. M., Dolan, C. V., & van der Maas, H. L. (2013). On the nature and nurture of intelligence and specific cognitive abilities: The more heritable, the more culture dependent. Psychological science, 24(12), 2420-2428. Retrieved from https://sci-hub.ru/https://doi.org/10.1177/0956797613493292

15. Kan, K. J. (2012). The nature of nurture: the role of gene-environment interplay in the development of intelligence (p. 134). Universiteit van Amsterdam [Host]. Retrieved from https://pure.uva.nl/ws/files/1689258/101363_thesis.pdf

16. Jensen, A. R., & McGurk, F. C. (1987). Black-white bias in ‘cultural’and ‘noncultural’test items. Personality and individual differences, 8(3), 295-301. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/0191-8869(87)90029-8

17. Blum, D., & Holling, H. (2017). Spearman's law of diminishing returns. A meta-analysis. Intelligence, 65, 60-66. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2017.07.004

18. Breit, M., Brunner, M., Molenaar, D., & Preckel, F. (2022). Differentiation hypotheses of intelligence: A systematic review of the empirical evidence and an agenda for future research. Psychological Bulletin, 148(7-8), 518. Retrieved from https://not-equal.org/content/pdf/misc/Breit2022.pdf

19. Tucker-Drob, E. M., De la Fuente, J., Köhncke, Y., Brandmaier, A. M., Nyberg, L., & Lindenberger, U. (2022). A strong dependency between changes in fluid and crystallized abilities in human cognitive aging. Science Advances, 8(5), eabj2422. Retrieved from https://www.science.org/doi/epdf/10.1126/sciadv.abj2422

20. Gignac, G. E. (2014). Dynamic mutualism versus g factor theory: An empirical test. Intelligence, 42, 89-97. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2013.11.004

21. Norman, G. (2024). The Stability Of g With Time. Half-Baked Thoughts. Retrieved from https://werkat.substack.com/p/the-stability-of-g-over-time

22. Norman, G. (2022). Learning, Memory, Knowledge, & Intelligence. Half-Baked Thoughts. Retrieved from https://werkat.substack.com/p/learning-memory-knowledge-and-intelligence-14a

23. Stuebing, K. K., Barth, A. E., Molfese, P. J., Weiss, B., & Fletcher, J. M. (2009). IQ is not strongly related to response to reading instruction: A meta-analytic interpretation. Exceptional children, 76(1), 31-51. Retrieved from https://sci-hub.ru/https://doi.org/10.1177/001440290907600102

24. Bergold, S., & Steinmayr, R. (2024). The interplay between investment traits and cognitive abilities: Investigating reciprocal effects in elementary school age. Child Development, 95(3), 780-799. Retrieved from https://srcd.onlinelibrary.wiley.com/doi/epdf/10.1111/cdev.14029

25. Schroeders, U., Schipolowski, S., & Wilhelm, O. (2015). Age-related changes in the mean and covariance structure of fluid and crystallized intelligence in childhood and adolescence. Intelligence, 48, 15-29. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2014.10.006

26. Kranzler, J. H., & Jensen, A. R. (1989). Inspection time and intelligence: A meta-analysis. Intelligence, 13(4), 329-347. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/S0160-2896(89)80006-6

27. Meldrum, R. C., Young, J. T., Kavish, N., & Boutwell, B. B. (2019). Could peers influence intelligence during adolescence? An exploratory study. Intelligence, 72, 28-34. Retrieved from https://sci-hub.ru/https;//doi.org/10.1016/j.intell.2018.11.009

28. Te Nijenhuis, J., & van der Flier, H. (2013). Is the Flynn effect on g?: A meta-analysis. Intelligence, 41(6), 802-807. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2013.03.001

29. Woodley, M. A., te Nijenhuis, J., Must, O., & Must, A. (2014). Controlling for increased guessing enhances the independence of the Flynn effect from g: The return of the Brand effect. Intelligence, 43, 27-34. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2013.12.004

30. Blankson, A. N., & McArdle, J. J. (2015). Measurement invariance of cognitive abilities across ethnicity, gender, and time among older Americans. Journals of Gerontology Series B: Psychological Sciences and Social Sciences, 70(3), 386-397. Retrieved from https://sci-hub.ru/https://doi.org/10.1093/geronb/gbt106

31. Wicherts, J. M., Dolan, C. V., Hessen, D. J., Oosterveld, P., Van Baal, G. C. M., Boomsma, D. I., & Span, M. M. (2004). Are intelligence tests measurement invariant over time? Investigating the nature of the Flynn effect. Intelligence, 32(5), 509-537. Retrieved from https://gwern.net/doc/iq/2004-wicherts.pdf

32. Beaujean, A. A. (2006). Using item response theory to assess the Lynn-Flynn effect (Doctoral dissertation, University of Missouri-Columbia). Retrieved from https://not-equal.org/content/pdf/misc/Beaujean2006.pdf

33. Beaujean, A. A., & Osterlind, S. J. (2008). Using item response theory to assess the Flynn effect in the National Longitudinal Study of Youth 79 Children and Young Adults data. Intelligence, 36(5), 455-463. Retrieved from http://www.iapsych.com/iqmr/fe/LinkedDocuments/beaujean2008.pdf

34. Beaujean, A. A., & Sheng, Y. (2010). Examining the Flynn effect in the general social survey vocabulary test using item response theory. Personality and Individual Differences, 48(3), 294-298. Retrieved from http://www.iapsych.com/iqmr/fe/LinkedDocuments/beaujean2010.pdf

35. Wai, J., & Putallaz, M. (2011). The Flynn effect puzzle: A 30-year examination from the right tail of the ability distribution provides some missing pieces. Intelligence, 39(6), 443-455. Retrieved from http://www.iapsych.com/iqmr/fe/LinkedDocuments/wai2011.pdf

36. Pietschnig, J., Tran, U. S., & Voracek, M. (2013). Item-response theory modeling of IQ gains (the Flynn effect) on crystallized intelligence: Rodgers' hypothesis yes, Brand's hypothesis perhaps. Intelligence, 41(6), 791-801. Retrieved from http://www.iapsych.com/iqmr/fe/LinkedDocuments/pietsching2013.pdf

37. Fox, M. C., & Mitchum, A. L. (2014). Confirming the cognition of rising scores: Fox and Mitchum (2013) predicts violations of measurement invariance in series completion between age-matched cohorts. Plos one, 9(5), e95780. Retrieved from https://sci-hub.ru/https://doi.org/10.1371/journal.pone.0095780

38. Beaujean, A., & Sheng, Y. (2014). Assessing the Flynn Effect in the Wechsler scales. Journal of Individual Differences, 35(2), 63. Retrieved from https://gwern.net/doc/iq/2014-beaujean.pdf

39. Benson, N., Beaujean, A. A., & Taub, G. E. (2015). Using score equating and measurement invariance to examine the Flynn effect in the Wechsler Adult Intelligence Scale. Multivariate Behavioral Research, 50(4), 398-415. Retrieved from https://sci-hub.ru/https://doi.org/10.1080/00273171.2015.1022642

40. Must, O., & Must, A. (2018). Speed and the Flynn effect. Intelligence, 68, 37-47. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2018.03.001

41. Dutton, E., van der Linden, D., & Lynn, R. (2016). The negative Flynn Effect: A systematic literature review. Intelligence, 59, 163-169. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.intell.2016.10.002

42. Oberleiter, S., Patzl, S., Fries, J., Diedrich, J., Voracek, M., & Pietschnig, J. (2024). Measurement-Invariant Fluid Anti-Flynn Effects in Population—Representative German Student Samples (2012–2022). Journal of Intelligence, 12(1), 9. Retrieved from https://doi.org/10.3390/jintelligence12010009

43. Shaw, P., Greenstein, D., Lerch, J., Clasen, L., Lenroot, R., Gogtay, N. E. E. A., ... & Giedd, J. (2006). Intellectual ability and cortical development in children and adolescents. Nature, 440(7084), 676-679. Retrieved from https://sci-hub.ru/https://doi.org/10.1038/nature04513

44. Stine-Morrow, E. A., Manavbasi, I. E., Ng, S., McCall, G. S., Barbey, A. K., & Morrow, D. G. (2024). Looking for transfer in all the wrong places: How intellectual abilities can be enhanced through diverse experience among older adults. Intelligence, 104, 101829. Retrieved from https://doi.org/10.1016/j.intell.2024.101829

45. Gobet, F., & Sala, G. (2023). Cognitive training: A field in search of a phenomenon. Perspectives on Psychological Science, 18(1), 125-141. Retrieved from https://doi.org/10.1177/17456916221091830

46. Norman, G. (2022). Expert Opinion On Race, IQ, Their Validity, & Their Connection. Half-Baked Thoughts. Retrieved from https://werkat.substack.com/p/expert-opinion-on-race-iq-their-validity