Factor Analyses Of Mental Abilities
Oblique VS Hierarchical Model Fit
Something to consider:
If hierarchical g models perform equivalently in confirmatory factor analysis to oblique models where group factor correlations aren't explained by g, then this basically means the group factor correlations pass Spearman's vanishing-tetrads test.
In other words, hierarchical g models don't have to display superior CFA performance to vindicate g theory, it's actually a strong confirmation of g theory if they merely display equivalent CFA model fit. If hierarchical models have a significantly but negligibly-worse model fit, then g theory is a negligibly-incomplete picture of the structure of mental abilities.
When we survey the confirmatory factor-analytic literature, this is the picture we see it painting [1, p.148; 2, pp.5 & 7; 3, p.129; 4, table 3, models 2 & 3; & 5, p.89, table 4-5]. In the Woodcock-Johnson Revised edition, they used to base their rejection of g on differences in model fit, but the equivalence of model fit is evident even in the WJ-R standardization data [5, p.89, table 4-5]; fit differences range from non-existant to negligible. They don't actually run significance tests for differences in model fit, they just note that the hierarchical g fit is "lower". The difference in rmr is negligible however (.045 VS .053), and if we look at the factor correlations on the next page and run Spearman's vanishing-tetrads test, the mean absolute tetrad difference is only .0396, which is even stronger support for g than in Spearman's original paper.
One possible reaction to seeing this is to say “SeE?!?!?! fAcToR aNaLySiS iS aBLe To PoSiT iNfiNiTeLy-MaNy DiFfErEnT MoDeLs Of EqUiVaLeNt FiT!!!!!!” Such an objection is missing the forest for the trees. If the oblique model which best satisfies simple structure passes Spearman's vanishing-tetrads test, g is an objectively necessary feature for describing your dataset; the g-loadings of the group factors imply factor correlations which satisfy Thurstonian simple structure, at least in the oblique sense.
Now, there are cases where people will posit only two group factors (say, GF VS GC), thereby precluding the possibility of doing this test. Whenever this happens, we know from the CHC research program, objectively, that it is the multiple abilities theorists who are at fault for positing too few group factors rather than the g theorists who are at fault for positing too many. The most-comprehensive taxonomy of test content in the domain of mental abilities simply demands enough group factors to reasonably accommodate Spearman's test; the collinearity needed to posit fewer just isn't there.
This stated, it isn't the end of the world to have to compete against oblique models in bad datasets like these. The superiority of bifactor models to both hierarchical-g models and non-hierarchical oblique models is arguably an even-harder condemnation than the fact that g models outright achieve the univariate equivalent of the satisfaction of simple structure. Comparing bifactor models and oblique models is the proper way to evaluate g theory, giving both proper opportunity to capitalize upon what's unique about their respective underlying theories in order to try to achieve superior model fit to their respective alternatives.
In non-hierarchical models, group factors are allowed to correlate in the way that maximizes their ability to satisfy Thurstonian simple structure (i.e. correlations between group factors are minimized with the restriction that the correlations between group factors must be able to account for any examples of subtests correlating substantially with more than one group factor). This freedom that group models afford to the factor correlations allows the subtests to correlate with their respective group factors as highly as possible; higher than would be possible in hierarchical models during scenarios where the tetrads test fails.
Bifactor models on the other hand relax the proportionality constraint imposed in hierarchical models. Basically, If g only affects subtest performance by means of affecting some group factor, this is equivalent to imposing a constraint where a subtest's g-loading can't differ from what's implied by how the subtest loads on the group factor. Hierarchical models demand that all subtests on a given group factor be identical to each other in terms of the ratio of their g-loading to their s-loading, whereas bifactor models have no such unreasonable requirement (i.e. bifactor models aren't a strawman of g-theory the way hierarchical models are, as they actually allow for g + s to be things which exist at the group factor level of the hierarchy and for which subtests can vary in loading for reasons other than measurement error and subtest specificity).
Really though, the superiority of bifactor models is just the cherry on top. Again, if there aren't enough group factors to test the degree to which g satisfies simple structure, then it's the test battery that's the problem. Ironically, the existance of a large diversity of mental abilities necessitates g.
Addendum: Spearman’s Vanishing-Tetrads Test Explained:
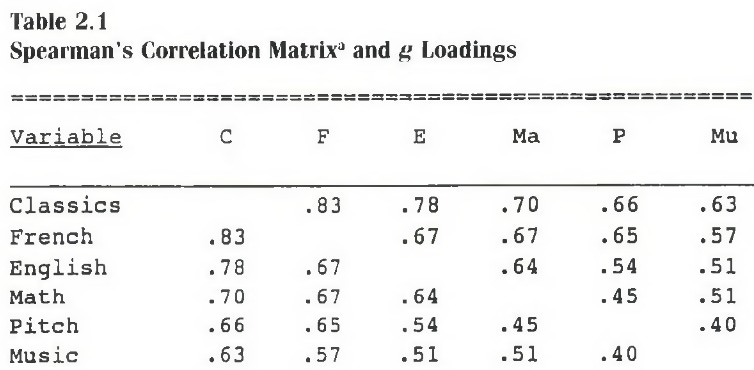
See this correlation matrix? Imagine you ignore all of the actual numerical entries, and just replace each entry with the product of the g-loadings of the two variables involved, whatever they happen to be. So for example, instead of .83, the correlation between French and classics would be assumed by g theory to be the g-loading of classics multiplied by the g-loading of French.
Now, repeat for the four entries where classics, french, math, and music intersect. What happens when we multiply the .7 entry by the .57 entry? We get the g-loading of classics multiplied by the g-loading of math and by the g-loading of music and by the g-loading of french and by the g-loading of music. What happens when we instead multiply the .63 entry by the .67 entry? We get the g-loading of classics multiplied by the g-loading of music and by the g-loading of French and by the g-loading of math. Notice anything? If g theory is true, the two different products are actually the same product of the same four g-loadings.
If we subtract these two products, g theory would predict the difference (what spearman called a tetrad difference) to be zero. If g theory is wrong on the other hand and classics and French are correlated to a larger or smaller degree than what would be implied by the g-loadings, then this tetrad difference wouldn't be zero.
A colleague of Spearman’s helped him come up with a statistical significance test for whether the mean absolute tetrad difference was significantly larger than what could be expected by chance. What was found at the time [6; see also 7, p.24] was that observed tetrad differences did not differ significantly. The average absolute tetrad difference in the table above was only 0.137. Now, these aren't actually quite the results you usually get in the factor analytic literature. The g factor does not account for 100% of common factor variance (although it does account for a supermajority). However, if you find the group factors which best satisfy simple structure for your battery, then the correlations between the group factors should pass the tetrads test, if not come very close. This is functionally what is implied when a hierarchical model fits equivalently to the oblique model from which it is derived.
References:
Golay, P., & Lecerf, T. (2011). Orthogonal higher order structure and confirmatory factor analysis of the French Wechsler Adult Intelligence Scale (WAIS-III). Psychological assessment, 23(1), 143. Retrieved from https://sci-hub.ru/https://doi.org/10.1037/a0021230
Dombrowski, S. C., McGill, R. J., & Canivez, G. L. (2018). An alternative conceptualization of the theoretical structure of the Woodcock-Johnson IV Tests of Cognitive Abilities at school age: A confirmatory factor analytic investigation. Archives of Scientific Psychology, 6(1), 1. Retrieved from https://psycnet.apa.org/fulltext/2018-07710-001.pdf
Sanders, S., McIntosh, D. E., Dunham, M., Rothlisberg, B. A., & Finch, H. (2007). Joint confirmatory factor analysis of the differential ability scales and the Woodcock‐Johnson Tests of Cognitive Abilities–Third Edition. Psychology in the Schools, 44(2), 119-138. Retrieved from https://sci-hub.ru/https://doi.org/10.1002/pits.20211
Chang, M., Paulson, S. E., Finch, W. H., Mcintosh, D. E., & Rothlisberg, B. A. (2014). Joint confirmatory factor analysis of the Woodcock‐Johnson tests of cognitive abilities, and the Stanford‐Binet intelligence scales, with a preschool population. Psychology in the Schools, 51(1), 32-57. Retrieved from https://sci-hub.ru/https://doi.org/10.1002/pits.21734
McGrew, K. S. (1994). Clinical interpretation of the Woodcock-Johnson Tests of Cognitive Ability--Revised. Boston: Allyn and Bacon. Retrieved from https://not-equal.org/content/pdf/misc/McGrew1994.pdf
Spearman, C. (1904). General Intelligence, Objectively Determined and Measured. American Journal of Psychology, 15, 201-293. Retrieved from https://sci-hub.ru/https://doi.org/10.2307/1412107
Jensen, A. R. (1998) The g factor: The science of mental ability. Westport, CT: Praeger, Vol. 648. Retrieved from https://emilkirkegaard.dk/en/wp-content/uploads/The-g-factor-the-science-of-mental-ability-Arthur-R.-Jensen.pdf