How Smart Is China?

IQ = 98.5778. Also, Whites are smarter than Asians.

TLDR:
—The National IQ of China is 98.5778.
—Our world’s White population has an average IQ of 99.45503.
—By genetic cluster analysis, Mongolia, Thailand, Cambodia, Vietnam, and Laos are East Asian just like China, Taiwan, North & South Korea, and Japan.
—Our world’s East-Asian population has an average IQ of 98.90467.

In this post I aim to calculate the national IQ of China using an approach similar to the World Bank Harmonized Test Scores or the Basic Skills dataset.

There exist two measures of IQ by Chinese province: One from the Chinese Family Panel Studies [1], and another from an iodine study where 38,000 people took a Raven’s test to see if iodine deficiency depresses intelligence [2, see 3]. Neither are normed in a way where scores make sense in an international context, but this at least enables us to say that if provinces A, B, and C have scores of 100, 102, and 106, then the A-C difference is triple the magnitude of the A-B difference. Given then a subset of provinces with an additional internationally-normed measure of intelligence, this later enables us to infer the internationally-normed test performance for all provinces and to then weigh by population to get the national IQ of China.

To synthesize the CFPS and Iodine study figures, I did a regression predicting the 2022 v8.1 subnational HDI differences between provinces, except for the Hainan, Ningxia, Qinghai, Tibet, and Xinjiang provinces wherein this was not possible due to missing CFPS values. Using the provinces with complete data, I took the predicted HDI values and fitted another regression equation predicting these from the Iodine figures and from observed HDI values. From there, in the provinces with missing CFPS values, I used the latter regression equation for imputation. The results are as follows:

Provincial HDI data from https://globaldatalab.org/shdi/table/shdi/?levels=1+4

International Contextualization:

There exist a couple resources which give internationally-normed scores for various Chinese provinces. First, there’s a study of PIRLS reading test scores for 23,143 rural Chinese students from the Shaanxi, Guizhou, and Jiangxi provinces [4]. Next, there’s the leaked 2009 PISA scores for the Tianjin, Shanghai, Beijing, Jiangsu, Zhejiang, Jilin, Hubei, Hebei, Hainan, Sichuan, Yunnan, and Ningxia provinces [5]; in this case we’re stuck with the limitation of having only the average across all 12 provinces, (hence dubbed the TSBJZJHHHSYN region) aside from Zhejiang and Shanghai which are also given individually. After that, we have the 2015 PISA scores for Beijing, Shanghai, Jiangsu, and Guangdong (BSJG) lumped together as a single region [6]. Finally, we have the 2018 PISA scores for the Beijing, Shanghai, Jiangsu, and Zhejiang (BSJZ) region [7]. For each test and for each PISA wave, we have several foreign nations that the provinces can be compared against, and so I standardized each according to Seb’s [8] national IQ estimates; in each case, national IQ would be regressed on (e.g., PISA 2009) test performance in order to assign ‘national IQ scores’ to provinces according to the predicted values. The result of doing so is as follows:

For comparison, our provincial IQ scores are also in the table. We don’t actually know if the multi-province regions are weighted by population or are just raw means, so for the provincial IQ scores, both scenarios are given. Here, correlation coefficients between provincial and international IQ scores are shown in scenarios where each region’s provincial IQ scores are either weighted by population or given as a simple mean:

We can see in each case that the provincial IQ scores line up more cleanly with the international IQ scores if it’s assumed that the international IQ scores aren’t weighted by population in the 2015 or 2018 PISA waves while they are in the 2009 leak. This leaves us to assume the following provincial equivalents:

Now, we can simply fit a regression equation predicting international IQ scores from provincial IQ scores and then generate predicted values for every province that lacks an international score, albeit anchored to the TSBJZJHHHSYN region since its provincial IQ score (0.8001645) is closest to the population-weighted mean of all provinces’ provincial IQ scores (0.7849439); provincial scores are multiplied by the unstandardized regression beta (264.2701) and then a -111.2165 intercept is subtracted to get international IQ scores (-111.2165 = 100.2430855 - 264.2701 * .8001645). This leaves us with the following internationally-contextualized IQ scores of each province:

The population-weighted mean of these is 96.22069. Now, a big reason for skepticism here is that these contextualized IQ scores have a provincial-level standard deviation of 12.68528. By contrast, the national-level standard deviation is only 10.94477:

If these results are to be believed, the smartest province (Beijing) has a 64.57365-point IQ lead on Tibet. Needless to say: No, the provincial IQ scores of China should not vary more than the international differences. Something to keep in mind is that when anchoring to the TSBJZJHHHSYN region, the regional IQ is slightly larger than the population-weighted national mean, which means that as the provincial-level standard deviation increases, the contextualized national mean decreases. Now, the national mean isn’t *that* sensitive to the standard deviation when we use the TSBJZJHHHSYN region as an anchor, but we can see what happens when we coerce the data to have some other standard deviation.

When looking at the provinces which have provincial IQ scores from both the CFPS and iodine studies, the iodine-study standard deviation was 5.920546 and the CFPS standard deviation was 4.888738, meanwhile my synthesis of the two had a standard deviation of 0.0384936. If we average the two standard deviations (5.404642) and take them as a percentage of the synthesis variable’s standard deviation (0.0384936), we get 140.4037. Using 140.4037 in place of the unstandardized beta from before, we get an intercept of -12.10297 (-12.10297 = 100.2430855 - 0.8001645 * 140.4037). Applying this regression equation to all the provinces, we get contextualized IQ scores as follows:

For these scores, the population-weighted national average is 98.10605 while the provincial standard deviation is a more-reasonable 6.739547 (and yes, this still leaves us with a provincial standard deviation of 5.40464 when considering only provinces possessing CFPS scores), although this standard deviation may still be a bit high.

What Went Wrong?

98.10605 is probably more reasonable, but we ideally shouldn’t be relying a coerced standard deviation like this. Moreover, if the problem is a result of some of the PIRLS or PISA scores being unreliable, it’s also not even clear if it’s reasonable to use the TSBJZJHHHSYN region as an anchor.

What if we just used the PIRLS scores from the Shaanxi, Guizhou, and Jiangxi provinces? Here they are again:

Notice anything? Jiangxi and Guizhou have essentially no IQ gap in the PIRLS data despite having a pretty major one in the provincial data. By contrast, Shaanxi and Jiangxi have a 10-point IQ gap in the PIRLS data despite having a smaller provincial IQ gap than the Jiangxi-Guizhou difference. The PIRLS data does not align at all with the provincial IQ data. Another bad sign comes from another study [9] assessing the IQ of rural Chinese people (not that we can use it since it doesn’t give an appropriate provincial breakdown) where performance averaged at 88.95. For what little it’s worth considering k=3, the provincial-international correlation here is r = 0.8168918. By contrast, the leaked 2009 PISA data works a lot better (r = 0.9995833 assuming the TSBJZJHHHSYN region is not population-weighted and r = 0.9992945 assuming it is):

The Shanghai-Zhejiang international score gap as a percentage of the provincial score gap is 9023.394% while for the Shanghai-TSBJZJHHHSYN difference it’s 10390.07% and it’s 10760.02% for the Zhejiang-TSBJZJHHHSYN difference. As we can see, whatever difference we’d use to replace the regression beta, it wouldn’t vary much. Using the data from all three provinces to find an unstandardized regression beta the normal way, we get 104.9044 = cor(intrntnl,provncl) * sd(intrntnl) / sd(provncl) rather than 90.23394 or 103.9007 or 107.6002. Contextualizing the provincial IQs of every province, once again anchored to the TSBJZJHHHSYN region, we get an intercept of +16.5451 (16.5451 = 100.2430855 - 104.9044 * 0.7978501) along with a population-weighted national IQ of 98.88917 and the much-more reasonable provincial standard deviation of 5.035538; the provinces are as follows:

Now, as it turns out, when we add the BSJG region from the 2015 PISA to the 2009 data (it works a fair bit better assuming BSJG is population weighted; r = +0.9982361 versus r = +0.8676147), it makes essentially no difference to how PISA lines up with the provincial IQ scores. By contrast, adding the BSJZ region from the 2018 PISA wave has a much more terrible effect (r = +0.6237657 assuming BSJZ is population weighted versus r = +0.7884545 otherwise). Whether assuming population weighting or a simple average, the provincial IQ score for BSJZ as a region is slightly lower than for either Shanghai or Zhejiang, and yet the 2018 PISA wave breaks with the prior two by giving the BSJZ region an IQ of 111.4379377 despite there being very little variation in provincial IQ among the four provinces; adding BSJZ outright breaks the perfection of the rank-order correlation.

It’s tempting to trichotomize the international scores into a PIRLS group, a 2009 PISA leak group, and a leftover group with the 2015 and 2018 PISA results. Assuming population-weighted results (0.8025825 for BSJG versus 0.8358373 for BSJZ) instead of simple means (0.8303815 for BSJG versus 0.8485742 for BSJZ) maximizes the provincial difference and thus minimizes the international difference as a percentage of the provincial difference, thereby minimizing the provincial standard deviation once we produce international IQ scores for all provinces. Here, since we can’t use the TSBJZJHHHSYN region, we’ll use BSJG for anchoring. We’ll use 333.8272 for our regression beta (333.8272 = (111.4379377 - 100.3365805) / (0.8358373 - 0.8025825)) and -167.5873 for our intercept (-167.5873 = 100.3365805 - 0.8025825 * 333.8272). With this regression equation, we get a population-weighted national IQ of 94.44831 and a provincial standard deviation of 16.02411:

Again, the 2018 PISA results are clearly out of line with all other PISA waves no matter how you slice it. It’s not simply a matter of the 2009 leak doing its own thing while Guangdong has a massive impact due to its large share of the region’s population paired with an enormous rural-urban divide; a rural-urban divide of the needed magnitude would eclipse both the nation-nation standard deviation and the individual-level standard deviation of IQ.

Now, seeing as the 2015 PISA wave is consistent with the 2009 leaks, we may as well try contextualizing the provincial IQ scores one more time to see what little difference it makes. With Shanghai, Zhejiang, BSJZ, and TSBJZJHHHSYN all together, the unstandardized regression beta is 111.097 while the intercept is +11.34721. As such, with performance contextualized internationally, the provinces score as follows:

The population-weighted national mean is 98.55212 while the provincial standard deviation is 5.33279. As far as I’m concerned, this is the best possible estimate of the national IQ of China. One thing to fix however: This doesn’t include Macao or Hong Kong, which we can infer from the 2009 PISA results to have international IQ scores of 98.73009383 and 103.3612542 respectively. These special administrative regions have populations of only 0.6788 million and 7.536 million respectively so it makes essentially no difference, but it brings the population-weighted mean up to 98.5778 while bringing the provincial standard deviation down to 5.25532.

European Versus Asian Intelligence:

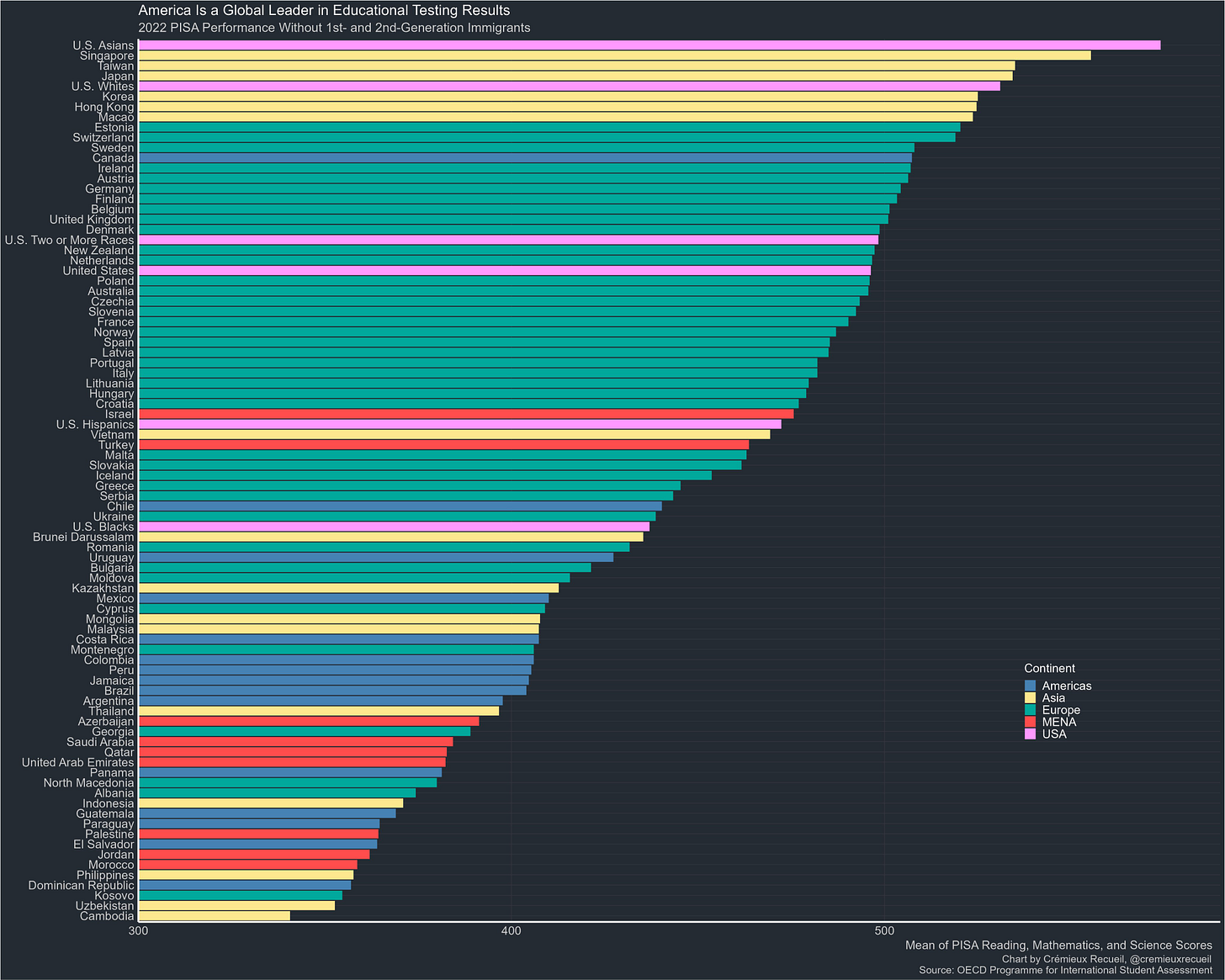
Something to keep in mind is that White countries have lots of minorities around and that the White people in those countries are smarter than the national IQ scores of the countries. We can see this in the 2022 PISA results with the United States broken down by race and all other countries stripped of their first and second generation immigrants [see 10, 11, & 12]:

Note also that Whites from New Zealand score about the same as White Americans [13].

Converting to national IQ, White Americans score 103.9733385 on average:

Obviously, we should trust the national IQ scores above what we’d infer them to be from PISA results, but the PISA results are the best we have for inferring the difference between a country’s national IQ and the natives of the nation. As such, taking the national IQ scores and subtracting the PISA-based native-national score difference estimates (subtracting zero for countries with no estimate), and setting China to a national IQ of 98.5778 while setting American and New Zealander Whites to an IQ of 103.9733385 and setting Asian Americans to 109.836, we get the following IQ estimates:

Based on cluster analyses [see 14 - Figure 1 & Extended-Data Figure 3, & 15 - Figure 1], I’m including Mongolia, Thailand, Cambodia, Vietnam, and Laos as “East Asian” while excluding Turkey from Europe.

Weighted by population, these figures give an average IQ of 99.45503 among White people while giving one of 98.90467 among East Asians.

References:

1. Jensen, S. (2023). IQ of China. sebjenseb. Retrieved from https://sebjenseb.net/p/iq-of-china

2. Li, Y., Wang, D., Su, X.-H., & Zhang, S.-B., & Yu, J.. (2006). Surveillance on iodine deficiency disorders in China in 2005: An analysis of intelligence test. Chinese Journal of Endemiology, 25(4), 430-433. Retrieved from https://gwern.net/doc/iodine/2006-li.pdf

3. Jensen, S. (2025). Answering questions on regional IQs. sebjenseb. Retrieved from

   https://sebjenseb.net/p/answering-questions-on-regional-iqs

4. Gao, Q., Wang, H., Chang, F., Yi, H., & Shi, Y. (2021). Reading achievement in China’s rural primary schools: A study of three provinces. Educational Studies, 47(3), 344-368. Retrieved from https://sci-hub.ru/https://doi.org/10.1080/03055698.2019.1701994

5. Karlin, A. (2012). Analysis Of China’s PISA 2009 Results. Anatoly Karlin. Retrieved from https://akarlin.com/analysis-of-chinas-pisa-2009-results/

6. Pisa, O. E. C. D. (2016). PISA 2015 Results (Volume I): Excellence and equity in education. PISA, OECD Publishing. Retrieved from https://www.oecd.org/content/dam/oecd/en/publications/reports/2016/12/pisa-2015-results-volume-i_g1g7397c/9789264266490-en.pdf

7. Pisa, O. E. C. D. (2019). PISA 2018 Results (Volume I): What students know and can do. Organization for Economic Cooperation and Development (OECD): Paris, France. Retrieved from https://www.oecd.org/content/dam/oecd/en/publications/reports/2019/12/pisa-2018-results-volume-i_947e3529/5f07c754-en.pdf

8. Jensen, S., & Kirkegaard, E. O. W. (2024). National IQs and Socioeconomic Development. Retrieved from https://osf.io/preprints/psyarxiv/bx86g_v1

9. Zhao, Q., Wang, X., & Rozelle, S. (2019). Better cognition, better school performance? Evidence from primary schools in China. China Economic Review, 55, 199-217. Retrieved from https://sci-hub.ru/https://doi.org/10.1016/j.chieco.2019.04.005

10. Pisa, O. E. C. D. (2023). PISA 2022 Results (Volume I): : The State of Learning and Equity in Education. Organization for Economic Cooperation and Development (OECD): Paris, France. Retrieved from https://www.oecd.org/content/dam/oecd/en/publications/reports/2023/12/pisa-2022-results-volume-i_76772a36/53f23881-en.pdf

11. Recueil, C. (2023). What Went Into The Melting Pot? Cremieux Recueil. Retrieved from https://cremieux.xyz/p/what-went-into-the-melting-pot

12. Recueil, C. (2023). [@cremieuxrecueil]. (2023, December 5). Do European countries appear to perform worse than White Americans in standardized tests because of low-performing immigrants? [Tweet]. Twitter. Retrieved from https://twitter.com/remieuxrecueil/status/1732244687929360434

13. Recueil, C. (2023). [@cremieuxrecueil]. (2023, December 6). This 2018 PISA report on New Zealand is consistent with the idea that the U.S. leads the way in scores [Tweet]. Twitter. Retrieved from https://twitter.com/remieuxrecueil/status/1732461094604529775

14. Lazaridis, I., Patterson, N., Mittnik, A., Renaud, G., Mallick, S., Kirsanow, K., ... & Krause, J. (2014). Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature, 513(7518), 409-413. Retrieved from https://sci-hub.ru/https:/doi.org/10.1038/nature13673

15. Rosenberg, N. A., Pritchard, J. K., Weber, J. L., Cann, H. M., Kidd, K. K., Zhivotovsky, L. A., & Feldman, M. W. (2002). Genetic structure of human populations. science, 298(5602), 2381-2385. Retrieved from https://sci-hub.ru/https://doi.org/10.1126/science.1078311